机器学习-聚类

评判指标

轮廓系数(Silhouette Coefficient):
- 定义: 量化样本与自身聚类的紧密程度,以及与其他聚类的分离程度。取值范围为 [-1, 1]。基于样本与本聚类中心的平均距离以及样本与其他聚类中心的平均距离计算得出。
- 调用API: sklearn.metrics.silhouette_score
- labels: 样本的聚类标签
- X: 样本特征矩阵
- metric: 距离度量方法,默认为'euclidean'
- sample_size: 计算时使用的样本数量,可以加快计算速度
- random_state: 随机种子,保证结果可重复
连通性(Connectivity):
- 定义: 度量聚类结果中相邻样本是否在同一聚类中。取值范围 [0, 最大连通度]。
- 推导: 基于样本之间的邻近关系计算得出。
- 调用API: sklearn.metrics.connectivity
  - labels: 样本的聚类标签
  - X: 样本特征矩阵
  - metric: 距离度量方法,默认为'euclidean'
  - neighbor_mode: 邻居定义方式,如'radius'或'kneighbors'
  - n_neighbors: 邻居数量,当 neighbor_mode='kneighbors' 时使用
Calinski-Harabasz指数:
- 定义: 度量聚类内部紧密度和聚类间分离度的比值。值越大表示聚类效果越好。
- 推导: 基于聚类内部平方和与聚类间平方和的比值计算得出。
- 调用API: sklearn.metrics.calinski_harabasz_score
  - labels: 样本的聚类标签
  - X: 样本特征矩阵
Davies-Bouldin指数:
- 定义: 度量聚类内部离散度与聚类间分离度的比值。值越小表示聚类效果越好。
- 推导: 基于聚类内部方差和聚类中心距离的比值计算得出。
- 调用API: sklearn.metrics.davies_bouldin_score
- labels: 样本的聚类标签
- X: 样本特征矩阵

Kmeans

聚类简单地讲就是将数据根据其位置信息得出一个标签。Kmeans通过先随机找到k个点，遍历每个数据，将每个数据归为距离自己最近的中心点为一类，分类完成后，计算k个类的均值（kmeans），更新这k个点，一直迭代直到收敛

对于给定的样本集，按照样本之间的距离大小，将样本集划分为K（k为输入）个簇。假设簇划分为 $(C_{1}, ... , C_{k})$ 则优化目标为最小化平方误差 $E$ $E=\sum\limits^{k}_{i=1}\sum\limits_{x \in C_{i}}\|x - \mu_{i}\|^{2}_{2})$ 其中 $\mu_{i}$ 是簇 $C_{i}$ 的均值向量（质心） $\mu_{i}=\frac{1}{C_{i}}\sum\limits_{x\in C_{i}}x$ 这是一个NP难的问题，需要使用启发式迭代找到解

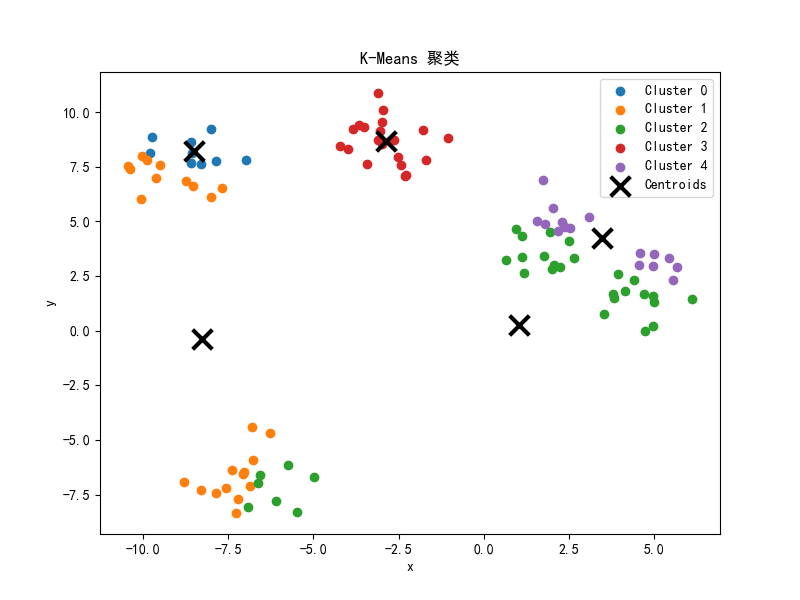
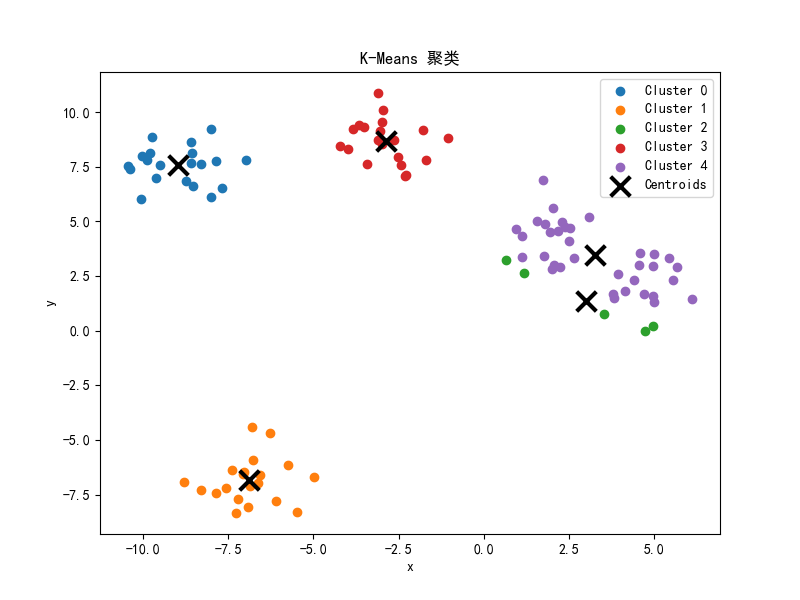
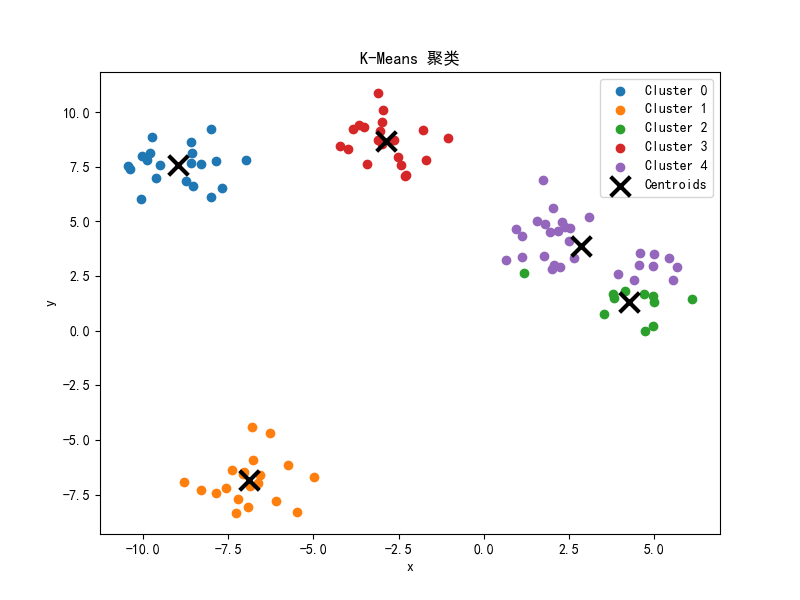
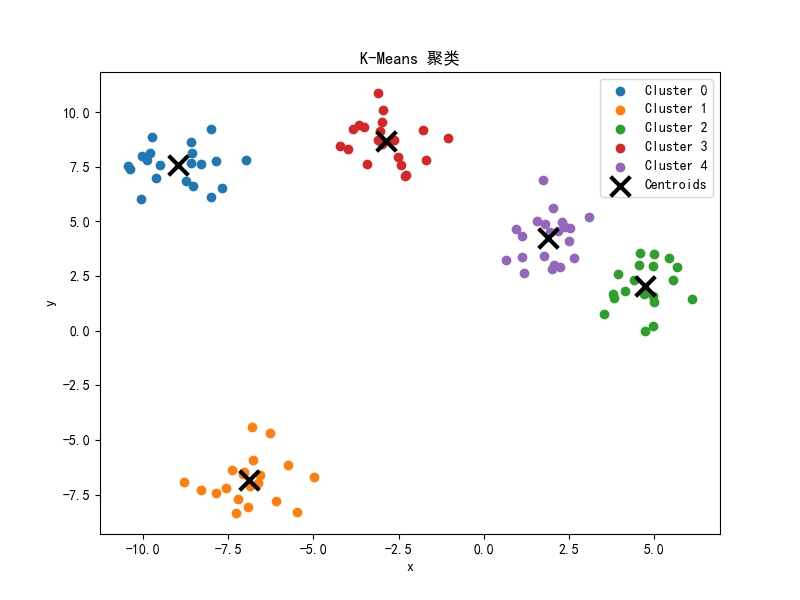
如图 ![[./img/传统kmeans聚类_1.png|400]] ![[./img/传统kmeans聚类_2.png|400]] ![[./img/传统kmeans聚类_3.png|400]] ![[./img/传统kmeans聚类_4.png|400]] 从图中可以看到，每次分类都通过计算新的类别平均值来更新原来的 $\mu$ 最终的效果非常不错

使用时，K值对计算结果影响很大，一般根据先验知识寻找一个K值，没有的话就通过交叉验证选择一个合适的随机K个点，这K个点需要尽量分散

对于输入的数据 $D=\{x_{1}, ..., x_{m}\}$ 簇的数量 $K$ 最大迭代数 $N$

从数据集中随机选取 $K$ 个样本作为质心 $\{\mu_{1}, ... , \mu_{k}\}$
对于 $n = 1, ..., N$ $n = 1, ..., N$ 遍历迭代次数
1. 初始化 $C_{t} \ t\in \{1, 2, ..., k\}$ 为空集
2. 对于 $x_{i} \ i = 1, ... m$ 计算 $x_{i}$ 到 $\mu_{j}$ 的距离 $d_{ij}=\|x_{i}-\mu_{j}\|^{2}_{2}$ ，将 $x_{i}$ 归为最小的 $d_{ij}$ 对应的类，即更新 $C_{j}=C_{j} \cup \{x_{i}\}$
3. 计算每个类别的平均值并更新 $\mu_{j}$ 即 $\frac{1}{C_{j}}\mu_{i}=\sum\limits_{x\in C_{j}}x$
4. 当没有 $\mu_{j}$ 被更新时，退出循环
输出簇划分

Kmeans ++

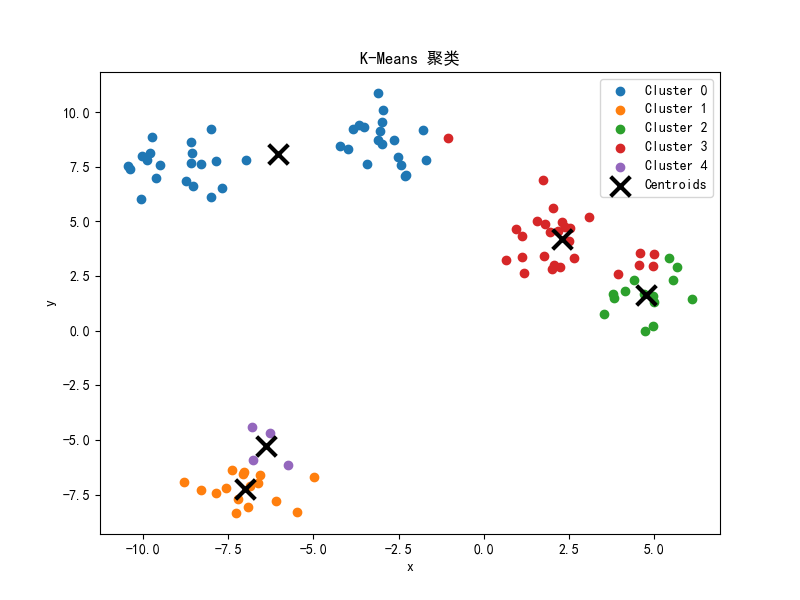
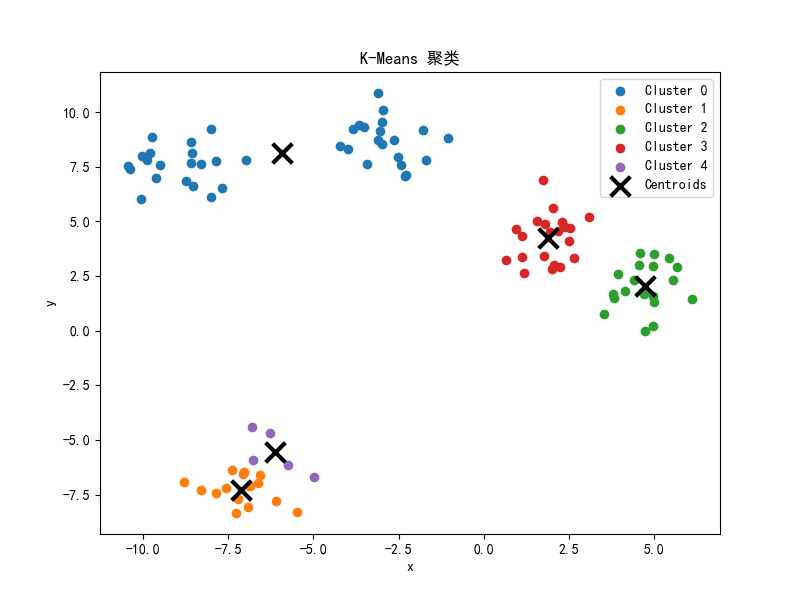
前面的Kmeans有时会有一些问题，如下 ![[./img/传统Kmeans失败_1.png|400]] ![[./img/传统Kmeans失败_2.png|400]] 可以看到直到最后也没有得到一个满意的结果。为什么呢？因为最开始的随机点选取得不太好，左下角的两个点挨得太紧了，这直接导致分类的结果不理想，不管最后怎么计算 $\mu$ ，都无法往理想的方向前进，就像一些人的人生一样，一旦出生，无论怎么努力都无法圆满:(

如何解决呢？关键在于最开始的点选得不好，我们希望最开始选的点尽量分开点，kmeans++的思想就是这样

随机选取一个点 $\mu_{1}$ $μ_{1}$
1. 计算每个数据点 $x_{i} \ i = 1, ... , m$ 到质心的距离计算 $D(x_{i}) = argmin\|x_{i}-\mu_{r}\|^{2}_{2} \ r = 1, ... , k_{selected}$ 即每个点到各个中心的最短距离作为值 $D$
2. 根据 $D$ 来选取下面的质心 $D(x_{i})$ 的值越大 $x_{i}$ 被选取作为质心的概率就越大
3. 重复直到选取k个质心
使用这k个质心继续进行kmeans

总结

K-Means的主要优点有： 1）原理比较简单，实现也是很容易，收敛速度快。 2）聚类效果较优。 3）算法的可解释度比较强。 4）主要需要调参的参数仅仅是簇数k。 K-Means的主要缺点有： 1）K值的选取不好把握 2）对于不是凸的数据集比较难收敛 3）如果各隐含类别的数据不平衡，比如各隐含类别的数据量严重失衡，或者各隐含类别的方差不同，则聚类效果不佳。 4）采用迭代方法，得到的结果只是局部最优。 5）对噪音和异常点比较的敏感。原文cnblogs

DBSCAN (Density-Based Spatial Clustering of Applications with Noise 基于密度和噪声应用的空间聚类)

是一种基于密度的聚类算法,与之前的 K-Means 不同,它不需要提前指定聚类的簇数。DBSCAN 通过密度来识别簇,并能够自动发现噪声数据点。

算法输入 $\epsilon$ MinPts 分别代表邻域半径 和核心对象的样本个数阈值

下面是一些概念

$\epsilon$ 邻域

即 $N_{\epsilon}(x_{j})=\{x \in D|distance(x_{i}, x_{j}) <= \epsilon \}$ 可以想象成以这个点为圆心的圆包含的样本集合

核心对象

$\epsilon$ 领域内达到MinPts个样本的数据即 $|N_{\epsilon}(x_{j})|>MinPts$

密度直达

如果 $x_{i}$ 位于 $x_{j}$ 的 $\epsilon$ 邻域中，且 $x_{j}$ 是核心对象，则称 $x_i$ 由 $x_{j}$ 密度直达。注意反之不一定成立，除非且 $x_i$ 也是核心对象，核心对象 $x_{j}$ 的 $\epsilon$ 邻域内每个点都与 $x_{j}$ 密度直达

密度可达

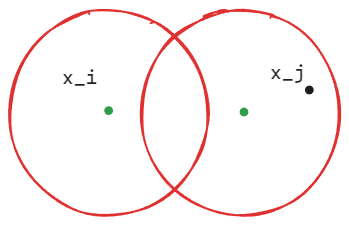
对于 $x_i$ 和 $x_j$ ,如果存在样本序列 $p_1,p_2,...,p_T$ ,满足 $p_1=x_i,p_T=x_j$ , 且 $p_{t+1}$ 由 $p_{t}$ 密度直达(这里 $p_{t}$ 是核心对象)，则称 $x_{j}$ 由 ${x_i}$ 密度可达，此时序列中的传递样本 $p_{1},...,p_{T−1}$ 均为核心对象。密度可达满足传递性，密度可达不满足对称性，这个可以由密度直达的不对称性得出。简单理解，一个核心对象和一个样本是否密度可达，就看二者之间能不能通过其他核心对象相连。下图就可以看到 $x_{i}$ 和 $x_{j}$ 就是密度可达的，二者有一个核心对象(绿色的点)对接 ![[./img/DBSCAN_密度可达.png|500]]

密度相连

对于 $x_i$ 和 $x_j$ ,如果存在核心对象样本 $x_k$ ，使 $x_i$ 和 $x_j$ 均由 $x_{k}$ 密度可达，则称 $x_i$ 和 $x_j$ 密度相连。这里就没有要求二者其中任何一个需要时核心对象了，因此密度相连关系是满足对称性的。

通过概念就可以大概知道DBSCAN要怎么做了，细想一下发现，其实一个密度相连的数据实际上就已经是一个簇了。具体做法就是找一个没有类别的核心对象，然后找到所有这个核心对象能够密度可达的样本集合，即为一个聚类簇。接着继续选择另一个没有类别的核心对象去寻找密度可达的样本集合，这样就得到另一个聚类簇。一直运行到所有核心对象都有类别为止。

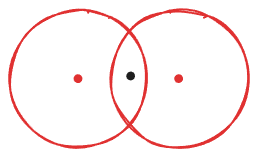
有三个特殊情况异常样本点：有些点不在任何一个核心对象在周围，在DBSCAN中，我们一般将这些样本点标记为噪音点。距离的度量问题。在DBSCAN中，一般采用最近邻思想，采用某一种距离度量来衡量样本距离，比如欧式距离。这和KNN分类算法的最近邻思想完全相同。对应少量的样本，寻找最近邻可以直接去计算所有样本的距离，如果样本量较大，则一般采用KD树或者球树来快速的搜索最近邻。第三种问题比较特殊，某些样本可能到两个核心对象的距离都小于ϵ，但是这两个核心对象由于不是密度直达，又不属于同一个聚类簇，不好判定类别（下图的黑点，两个核心对象不密度直达，属于不同类）。一般来说，此时DBSCAN采用先来后到，先进行聚类的类别簇会标记这个样本为它的类别。也就是说DBSCAN的算法不是完全稳定的算法。 ![[./img/DBSCAN_不稳定性.png|500]]

总结

和传统的K-Means算法相比，DBSCAN最大的不同就是不需要输入类别数k，当然它最大的优势是可以发现任意形状的聚类簇，而不是像K-Means，一般仅仅使用于凸的样本集聚类。那么我们什么时候需要用DBSCAN来聚类呢？一般来说，如果数据集是稠密的，并且数据集不是凸的，那么用DBSCAN会比K-Means聚类效果好很多。如果数据集不是稠密的，则不推荐用DBSCAN来聚类。

下面对DBSCAN算法的优缺点做一个总结。 DBSCAN的主要优点有： 1）可以对任意形状的稠密数据集进行聚类，相对的，K-Means之类的聚类算法一般只适用于凸数据集。 2）可以在聚类的同时发现异常点，对数据集中的异常点不敏感。 3） 聚类结果没有偏倚，相对的，K-Means之类的聚类算法初始值对聚类结果有很大影响。 DBSCAN的主要缺点有： 1）如果样本集密度不均匀、聚类间距差相差很大时，聚类质量较差，这时用DBSCAN聚类一般不适合。 2）如果样本集较大时，聚类收敛时间较长，此时可以对搜索最近邻时建立的KD树或者球树进行规模限制来改进。 3）调参相对于传统的K-Means之类的聚类算法稍复杂，主要需要对距离阈值ϵ，邻域样本数阈值MinPts联合调参，不同的参数组合对最后的聚类效果有较大影响。