神经网络

感知机

原始形式的感知机是一种简单的线性分类模型，它通过找到一个分割超平面来将数据集分为两类。其数学模型可以表示为：
$f(x) = \text{sign}(w \cdot x + b)$
其中，$w$ 是权重向量，$b$ 是偏置项，
且 $\text{sign}$ 函数是符号函数，用于输出分类结果（+1 或 -1）。
在训练过程中，权重和偏置的更新规则如下：

• 如果 $y_i(w \cdot x_i + b) \leq 0$，即分类不正确 则：
  $w \leftarrow w + \eta y_i x_i$
  $b \leftarrow b + \eta y_i$
  这里的 $\eta$ 是学习率，$y_i$ 是实际的类别标签。

对偶形式感知机

之前提到$w$的更新方式是$w = w + \eta y_{i}x_{i}$ ，如果初始$w$为零 则$w = \eta y_{i}x_{i}$，这里就可以看出来，$w$实际上就是每个数据的标签$y_{i}$和数据向量$x_{i}$作用的结果，每个数据一旦没有被正确分类就会对$w$作用很多次，下面我们通过一个变量$m_{j}$来记录数据$x_{j}$对$w$的作用次数，从而可以直接表示出$w$

迭代到最后 结果就是$w = \eta\sum\limits_{j=1}^{N}m_{j}y_{j}x_{j}$ （这里相比之前 添加了所有数据对$w$的影响，之前的也有只是没体现出来）

其中，$m_{j}$为$(x_{j}, y_{j})$在这次之前被错误分类的次数，初始为0

令$\alpha_{j}=m_{j}\eta$ 则 $w = \sum\limits_{j=1}^{N}\alpha_{j}y_{j}x_{j}$ 代入最开始的迭代式$y_i(w \cdot x_i + b) \leq 0$，得到$y_i(\sum\limits_{j=1}^{N}\alpha_{j}y_{j}x_{j} \cdot x_i + b) \leq 0$
注意到这个判断误分类的形式里面是计算两个样本$x_{i}$和$x_j$的内积，而且这个内积计算的结果在下面的迭代次数中可以重用。如果我们事先用矩阵运算计算出所有的样本之间的内积，那么在算法运行时， 仅仅一次的矩阵内积运算比多次的循环计算省时。 计算量最大的判断误分类这儿就省下了很多的时间，，这也是对偶形式的感知机模型比原始形式优的原因。

之后迭代试如下

• 如果 $y_i(\sum_{j=1}^N \alpha_j y_j x_j \cdot x_i + b) \leq 0$ 其中（$\sum\limits_{j=1}^{N}\alpha_{j}y_{j}x_{j} = w$）， 则：
  $\alpha_i \leftarrow \alpha_i + \eta$（$\alpha_{j}=m_{j}\eta$）
  $b \leftarrow b + \eta y_i$
  收敛后通过公式$w = \eta\sum\limits_{j=1}^{N}m_{j}y_{j}x_{j}$得到权值向量$w$
  参考 刘建平感知机模型

DNN(Deep Neural Network)模型推导

神经网络的基本单元是感知机，但通过增加隐藏层和非线性激活函数，神经网络能够处理更加复杂的非线性问题。

神经网络的结构

1. 输入层：接收输入数据。
2. 隐藏层：通过权重和激活函数进行计算。
3. 输出层：生成最终的预测结果。

参数的定义

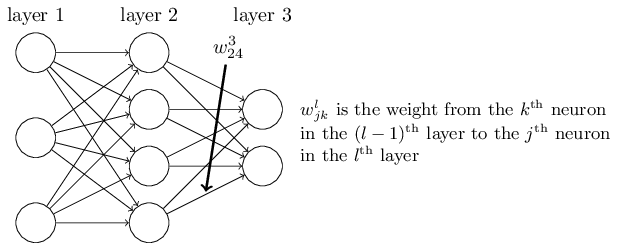
在神经网络中，权重 ( w ) 和偏置 ( b ) 是需要学习的参数。权重 $w_{ij}^l$ 表示从第 $l$ 层的第 $j$ 个神经元到第 $l+1$ 层的第 $i$ 个神经元的连接权重。

权重 $w_{24}^3$ 表示第二层的第4个神经元到第三层的第2个神经元的权重。上面代表第几层（从2开始，因为输入层没有变换），下面代表从哪个神经元到哪个神经元，这里是目的和来源相反的。每个$w$对应一个箭头（变换） ![[./img/神经网络参数w.png]]

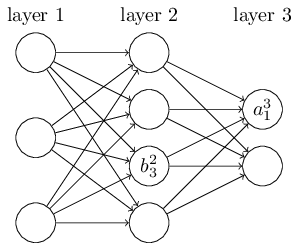
权重 $b_{3}^{2}$ 表示第二层的第3个神经元的偏移，上面的次数代表第几层，下面代表第几个神经元，参数b对应于某个神经元 ![[./img/神经网络参数b.png|500]]

前向传播

前向传播是指从输入层到输出层逐层计算神经元的输出值的过程。假设有一个三层神经网络（输入层、隐藏层、输出层），其计算过程如下： ![[./img/神经网络_向前传播.png|500]]

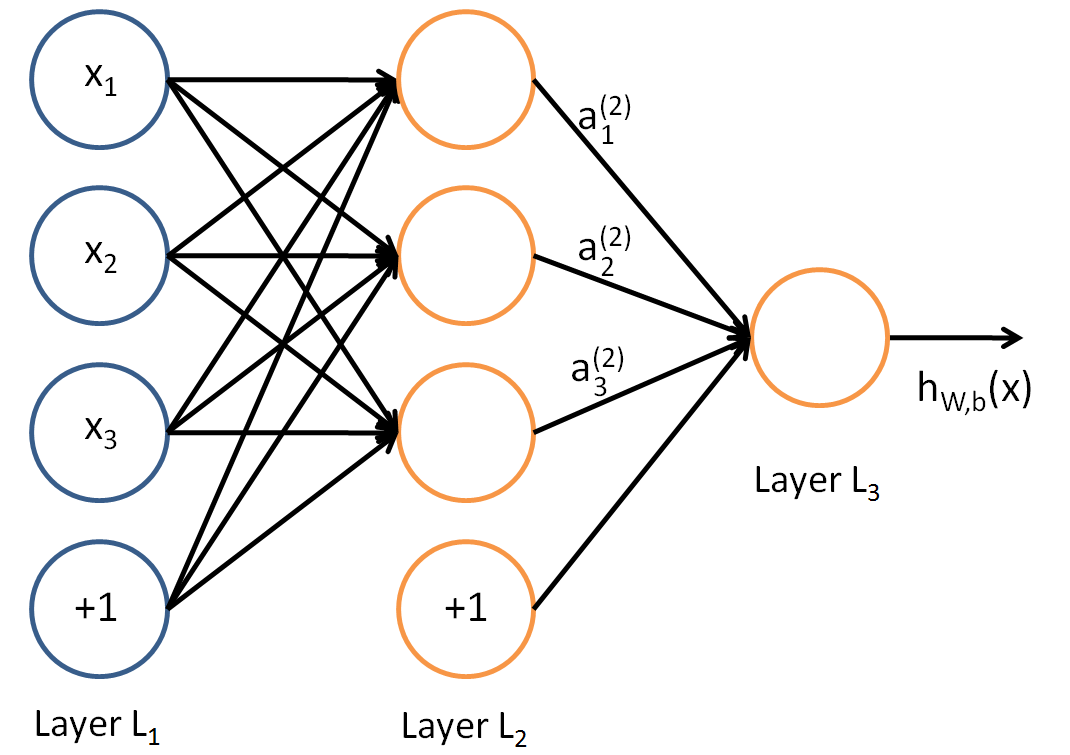
1. 输入层到隐藏层： $$\begin{aligned} a_{1}^{2} = \sigma(z_{1}^{2}) = \sigma(w_{11}^1 x_1 + w_{12}^1 x_{2}+ w_{13}^1 x_2+ b_{1}^{2})\\ a_{2}^{2} = \sigma(z_{2}^{2}) = \sigma(w_{21}^1 x_1 + w_{22}^1 x_{2}+ w_{23}^1 x_2+ b_{2}^{2})\\ a_{3}^{2} = \sigma(z_{3}^{2}) = \sigma(w_{31}^1 x_1 + w_{32}^1 x_{2}+ w_{33}^1 x_2+ b_{3}^{2}) \end{aligned}$$
2. 隐藏层到输出层： $a_{1}^{3} = \sigma(z_{1}^{3}) = \sigma(w_{11}^3 a_{1}^{2} + w_{12}^{3} a_{2}^{2}+ w_{13}^3 a_{2}^{3}+ b_{1}^{3})$ 其中，$\sigma$ 表示激活函数（如Sigmoid、ReLU等）。 这里可以简单转化为 $$a_{j}^{l}= \sigma(z_{j}^{l})= \sigma(\sum\limits_{k=1}^{m}w_{jk}^{l}a_{k}^{l-1}+b_{j}^{l})$$ 其中m代表前一层神经元的个数，这里$l$要大于等于2，当$l=2$时，$a_{k}^{0}$代表输入$x_{1}, ..., x_{n}$ 进而转换成矩阵形式 $$a^{l} = \sigma(z^{l}) = \sigma(w^{l}a^{l-1}+b^{l})$$

反向传播

在这个问题中，您想要了解如何从损失函数 $J(W, b, x, y)$ 对权重 $W^L$ 和偏置 $b^L$ 的导数推导过程。

损失函数

损失函数 $J$ 定义为均方误差:

其中 $a^L$ 是输出层的激活值,$z^L$ 是输出层的加权输入,即 $z^L = W^L a^{L-1} + b^L$。

对权重 $W^L$ 的梯度

为了计算 $\frac{\partial J}{\partial W^L}$,我们需要使用链式法则。首先,从损失函数对输出层激活 $a^L$ 的偏导数开始:

接着,我们需要 $a^L$ 对 $z^L$ 的偏导数,这是激活函数 $\sigma$ 的导数:

根据链式法则,$\frac{\partial J}{\partial z^L}$ 为:

称这个结果为误差 $\delta^L$:

最后,$z^L$ 对 $W^L$ 的偏导数是前一层的激活 $a^{L-1}$,因此:

对偏置 $b^L$ 的梯度

类似地,$z^L$ 对偏置 $b^L$ 的偏导数是一个单位向量($z^{L}= W^L a^{L-1} + b^L$，偏置的梯度是误差 $\delta^L$),因此:

递推

在实际应用中，知道$\delta^{l+1}$（最开始是$\delta^{L}$）后，要知道$\delta^{l}$需要使用数学归纳法

其中，$\frac{\partial z^{l+1}}{\partial z^{l}}$需要推导 $z^{l+1} = W^{l+1} a^{l} + b^{l}=W^{l+1}\delta(z^{l})+b^{l}$ 对$z^{l}$进行求导

从而

因此只需要求出最后一层的$\delta^{L}$就可以推导出前面的