介绍

PCA的目的是找到一个矩阵将数据降维的同时最大程度保留原始数据的信息通过证明可以得出这个矩阵就是原数据(标准化)协方差矩阵的特征向量矩阵 协方差(covariance)矩阵 $cov$ 定义为 $cov_{i,j}=\frac{1}{m}\sum\limits_{i,j}^{m}(x_{i}-\mu)^{T}(x_{j}-\mu)$ 如果数据集 $X \in R^{n*d}$ 则 $cov \in R^{d*d}$ 也可以是 $cov \in R^{n*n}$ 前者反应了各个特征之间的变化关系对角线为各个特征的方差特征向量矩阵更加易于理解后者反应了各个数据的差异对角线是数据的二范数特征向量矩阵比较抽象但仍然包含了主成分当数据量小于特征数量的时候使用后者协方差选取不同后面降维时映射矩阵乘的方向就不同

其中a和b是特征序号因为数据是标准化后的因此 $\mu_{i}$ 为0

推导

可以从两个方面出发进行证明

最小化重构误差

数据 $X \in R^{d*n}$ 投影矩阵 $A \in R^{d*r}$ 投影后 $A^{T}X$ 再重构恢复数据为 $AA^{T}X$ 希望恢复后与原来的数据差距最小等价于

argmin_{A}\|X-AA^{T}X\|_{F}^{2} \ s.t.A^{T}A=I

\begin{aligned} &\|X-AA^{T}X\|_{F}^{2} \\ &=tr[(X-AA^{T}X)^{T}(X-AA^{T}X)] \\ &=tr[X^{T}X-2X^{T}AA^{T}X+AA^{T}X^{T}AA^{T}X]\\ &=tr(2X^{T}X-2X^{T}AA^{T}X) \end{aligned}

其中 $X^{T}X$ 为定值原式等价

argmax_{A}tr(A^{T}XX^{T}A) s.t. A^{T}A=I

最大化散度

argmax_{A}\|A^{T}X-A^{T}\mu\|_{F}^{2} \ s.t.\ A^{T}A=I

其中 $\mu=\frac{1}{n}\sum\limits_{i=1}^{n}(x_{i})$ ,原数据经过归一化，平均值为0 则原式

\begin{aligned} &\|A^{T}X\|_{F}^{2}\\ &=tr(A^{T}XX^{T}A) \end{aligned}

即二者都等价于

argmax_{A}tr(A^{T}XX^{T}A)\ s.t. \ A^{T}A=I

构造拉格朗日函数并对 $A$ 求偏导令其为0

\begin{aligned} J(A, \lambda)&=tr(A^{T}XX^{T}A)-\lambda(A^{T}A-I)\\ \frac{\partial J}{\partial A}&=2XX^{T}A-2\lambda A=0\\ &\Rightarrow XX^{T}A =\lambda A \end{aligned}

这里的 $A$ 就是 $XX^{T}$ 的特征向量矩阵， $\lambda$ 为特征值矩阵( $diag(\lambda_{1}, ...,\lambda_{d})$ )

问题

计算完特征矩阵后，要将特征向量根据特征值进行排序进而选取前k(希望降到的维数)个特征向量，为什么要根据特征值选取特征向量？

选取特征向量时，肯定要优先选取包含信息最多的k个向量，因此这个问题就是为什么特征向量大就包含的信息多假设 $y_{1}$ 为第一个主成分则有 $y_{1}=\alpha_{i}^{T}X$ 其中 $\alpha_{i}$ 为含有信息量第一的的特征向量，有 $\alpha_{i}^{T}\alpha_{i}=1$ 我们希望 $y_{1}$ 的方差最大，其中y的方差

var(y_{1})=var(\alpha_{i}^{T}X)=E[(y_{1}-\mu')(y_{1}-\mu')^{T}]=\alpha_{i}E[(X-\mu)(X-\mu)]\alpha^{T}_{i}

其中间部分即为X的协方差矩阵记为 $\sum$ 则优化式为(这里限制条件是指 $\alpha_{i}$ 是一个单位向量)

\begin{aligned} argmax_{\alpha_{i}} \ &\alpha_{i}^{T}\sum\alpha_{i} \ s.t. \ \alpha_{i}\alpha_{i}^{T}=1 \\ J(\alpha_{i}, \lambda) &=\alpha_{i}^{T}\sum\alpha_{i} -\lambda(\alpha_{i}\alpha_{i}^{T}-1)\\ \frac{\partial J}{\partial \alpha_{i}}&=2\sum\alpha_{i}-2\lambda\alpha_{i}\\ &\Rightarrow \sum\alpha_{i}=\lambda\alpha_{i} \end{aligned}

结论带入原式

\alpha_{i}^{T}\sum\alpha_{i}=\alpha_{i}^{T}\lambda\alpha_{i}=\alpha_{i}^{T}\alpha_{i}\lambda=\lambda

也就是说方差等价于 $\lambda$ 即特征值特征值越大映射后的数据方差也就越大

下面继续证明第二个主成分 $y_{2}$ 对应的特征向量为第二大的特征值对应的向量待优化式(其中第二个限制条件是指特征向量每每正交)

\begin{aligned} argmax_{\alpha_{i}} \ &\alpha_{i}^{T}\sum\alpha_{i} \ s.t. \ \alpha_{i}\alpha_{i}^{T}=1,\alpha_{i}^{T}\alpha_{1}=0 \\ J(\alpha_{i}, \lambda, \theta)&=\alpha_{i}^{T}\sum\alpha_{i}-\lambda(\alpha_{i}^{T}\alpha_{i}-1)-\theta\alpha_{i}^{T}\alpha_{1} \\ \frac{\partial J}{\partial \alpha_{i}}&=2\sum\alpha_{i}-2\lambda\alpha_{i}-\theta\alpha_{1} \\ &=2\alpha_{i}^{T}\sum\alpha_{i}-2\lambda\alpha_{i}^{T}\alpha_{i}-\theta\alpha_{i}^{T}\alpha_{i}\\ &=0 \\ &\Rightarrow \theta=0 \\ 带入原式有 &\sum\alpha_{i}=\lambda\alpha_{i} \end{aligned}

从而同样可以得出降维后方差等于特征值的结论依次类推可以通过 $y_{k-1}$ 推得 $y_{k}$ 为特征矩阵时降维后方差与特征值的关系因此可以得出降维后的方差和特征值是等价的所以将特征值按降序排列后依次选取的特征向量就是包含信息量最多的前几个特征值

直觉上的理解

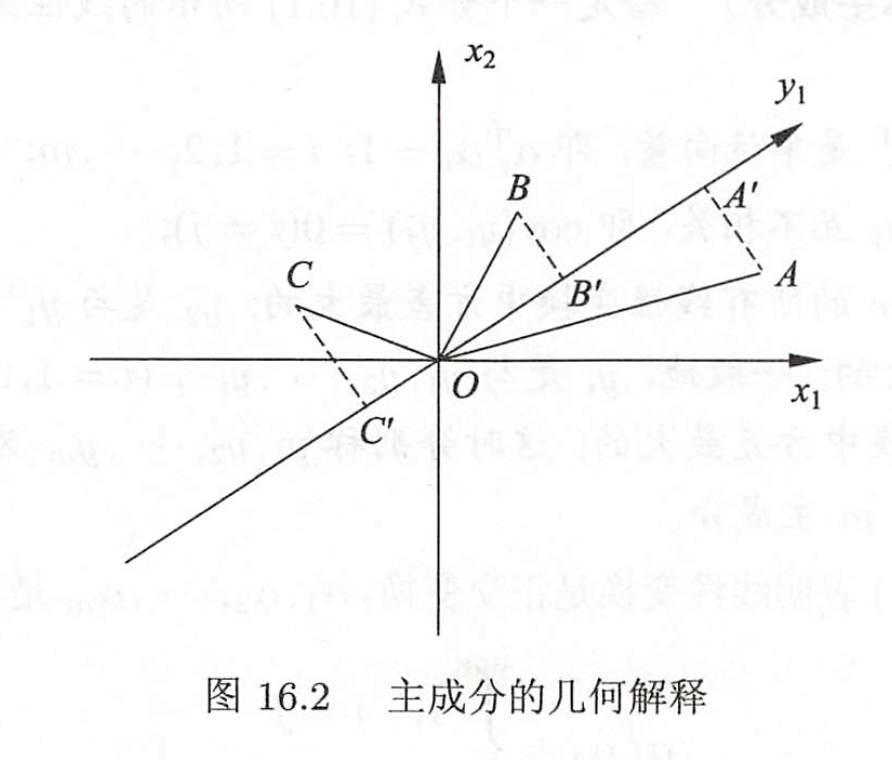
如下图，原数据A,B,C要投影到 $y_{1}$ ![[./img/PAC等价关系.png|500]] 假设数据已经经过归一化原数据的方差 $OA^{2}+OB^{2}+OC^{2}$ 固定最大化散度即最大化 $OA^{`}+OB^{`}+OC^{`}$ 在三角形 $OAA^{`}$ 中 OA固定最大化 $OA^{`}$ 即最小化 $A^{`}A$ 也就是最小化重构误差

pca原理1pca原理2 来源: 李航：统计学习方法(第二版)